https://wherwhen.tistory.com/3
선형회귀(Linear Regression) 이론 2 - 손실함수(Loss Function) 1
이전에는 선형회귀가 무엇인지, 그리고 선형회귀에 대한 가설함수까지 설명하였다. https://wherwhen.tistory.com/2 선형 회귀(Linear Regression) 이론 지도 학습의 한 유형이면서, 연속적인 값을 가지고 예
wherwhen.tistory.com
이전 글에서는 경사 하강법에 대한 개념과 설명을 했다면 이번글에서는 경사 하강법에 대한 예시와 계산을 설명하겠다.

이전 글에서 J와 기울기에 대해 설명을 했는데, 예시를 들어 설명하면 아래와 같이 Jθ에 대한기울기가 1θ,2θ인데 여기서 θ0,θ1이 3,2이라면 왼쪽과 같이 현재 기울기가 3,4인것을 구할 수 있다. 하지만 이 기울기는 현재 위치에서 가장 가파르게올라갈 수 있는 기울기이니까 가장 가파르게 내려가야 하는 우리에게는 반대되는 값이다. 즉 마이너스 부호를 붙여서 -3,-4가 되어야 하는것이다. 그리고 Jθ에 대한 값들은 각각 J를 θ0(1θ), θ1(2θ)으로 편미분한 값이다. 그럼 이제 여기서 새로운 θ에 대해서 조정을 해야하는데 이때 θ0 에 대해 무조건 마이너스 시켜서 내려가는게 아니라 학습률 α(알파)를 곱한
다음 빼야 한다. 즉 θ0 = -3-α*(-3)이라고 재정의 해주어야 한다. 이건 θ1에도 동일하게 적용하여야 한다.
여기서 학습률이란 얼마나 많이 혹은 적게 움직여야하는지 그 정도를 알려주는 수치이다. 학습률이 크다고 좋은것도,
작다고 나쁜것도 아니며 해당 output에 맞게 적절하게 잘 조절하여 학습률을 설정 해주어야 한다.
만약 학습률이 너무 크다면, 한번에 많이 움직이므로 오히려 극소점에서 빠르게 멀어질수도 있다.
학습률이 작다면 극소점으로 이동하는데 매우 오래 걸릴수도 있다.
그럼 여기서 학습률이 0.2라고 하면 θ0 = 3-0.2*(3) = 2.4가 될것이고, θ1=2-0.2*(4) =1.2가 될것이다. 즉 아래로 약간
내려간것을 볼 수 있다. 이걸 수식으로 나타내면 다음과 같다.
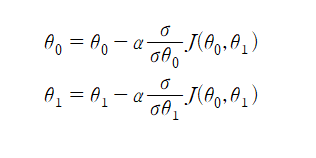
손실함수 J를 θ0에 대해서 편미분한 결과값에 알파를 곱하고 그걸 θ0에서 빼준값이며, 이걸 업데이트 했다고도 표현한다.
이건 θ1에 대해서도 동일하다. 하지만 여기서 θ1을 업데이트 할 때, θ0를 업데이트하고 넣는게 아니라 업데이트 이전의
θ0를 넣어줘야 한다. 그래야 θ1이 올바르게 업데이트 되기 때문이다. 위의 식을 편미분하면 다음과 같이 정리가 된다.

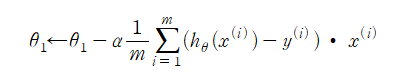
이렇게 가설함수를 데이터에 조금씩 맞춰 나갈 수 있는것이다. 이렇게 계속하다보면 언젠가는 극소점에 맞는(최적의) θ값을 찾을 수 있는것이고, 이는 곧 손실함수의 값도 줄여나갈 수 있다는 의미이기도 하다.
다음글에서는 이론적인 부분이 마무리 되었으니 가설함수, 예측오차, 경사 하강법에 대해서 코딩하고 설명하는 글이
될것이다.
'Mahcine Learning' 카테고리의 다른 글
| 선형회귀(LinearRegression) 가설함수, 손실함수, 경사하강법 설명 (0) | 2023.06.05 |
|---|---|
| 선형회귀(Linear Regression) 이론 2 - 손실함수(Loss Function) 1 (0) | 2023.05.27 |
| 선형 회귀(Linear Regression) 이론 1 (0) | 2023.05.25 |


