이전에는 각 노드를 생성하고 이를 서로 연결하여 그래프를 만드는 이론과 코딩을 설명하였다.
하짐나 이건 그래프의 아주 기초적인 단계이며, 이를 바탕으로 여러 그래프가 존재한다.
그 중 그래프를 나타내는 다른 표현을 설명하겠다.
인접행렬이란? 그래프를 2차원 행렬로 표현 한것으로 각 노드 중간에 존재하는 엣지의 연결성을
나타내는 리스트이다. 이 행렬은 노드수 X 노드수의 크기를 가지며, 각 노드들의 연결 관계를 나타내고 있다.
예를 들어 아래와 같은 그래프가 존재하다고 가정하자.

이 그래프는 어떠한 가중치도 존재하지 않는 그래프이다.
이 그래프를 이렇게 표현 할 수도 있지만, 행렬로 나타내면 다음과 같이 표현 할 수 있다.

각 노드들간의 관계를 0과 1로 표현하였다. 연결이 되어있으면 1, 연결이 되어있지 않으면 0으로 표현하였다.
여기서도 자세히 보면 각 노드들은 자신과는 연결 되지 않았기에 대각선 방향으로 모두 0으로 표현 되어있다.
이렇게 리스트만으로도 그래프를 표현 할 수 있고, 이러한 행렬을 이용하여 그래프를 나타낼 수 있다.
만약 가중치 그래프라면 0과 1이 아닌 각 엣지의 가중치가 담겨져 있을것이다.
위의 그래프와 리스트를 가중치 그래프로 변경하면 다음과 같다.
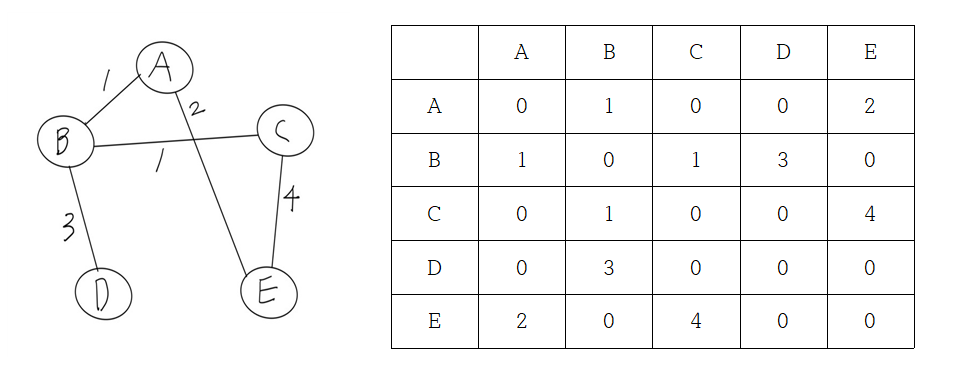
이렇게 위에서 표현만 했던 연결성이 아닌 가중치가 직접 들어가 있다.
만약 방향 그래프라면 이렇게 행렬로 나타낼 수 있다.

각 노드들에서 나가는 엣지만 표현하고 들어오는 엣지는 표현하지 않는다.
이러한 이론과 표현을 바탕으로 실질적인 코딩으로 나타내자

일단 처음으로 인접행렬의 크기를 노드수 x 노드수(5*5)로 초기화 시킨다.
그리고 각 노드들을 엣지로 연결 시키는데 이때, 처음에 0으로 초기화 시켰기때문에 서로 엣지가 연결된
노드만 1로 연결시켜주면 된다.
그리고 이렇게 연결된 인접행렬을 출력하면 된다.

그럼 위에서 언급한 2차원 리스트와 동일한 결과가 나오는것을 볼 수 있다.
'Graphy' 카테고리의 다른 글
| 그래프 만들고, 연결하기 (0) | 2023.06.23 |
|---|---|
| 그래프 이론 (0) | 2023.06.20 |

